Data Structure: Binary Heap[Max & Min] in JavaScript and TypeScript

by

A binary Heap is a special kind of tree. For a Binary Tree to be a Binary Heap the rule is simple-

Max Binary Heap– the parent node is always larger than the child nodes.
Min Binary Heap– The parent node is always smaller than the children.

As we can see, there are 2 types of Binary Heap- min and max.

NOTE

There is no rule for the nodes. There are no ordering guarantees between the siblings.
Binary Heap is very compact, as all nodes are as full as they can be.
The left node is filled first.

In this article, we are discussing the implementation of Binary Heap(both Min and Max) in JavaScript and TypeScript.

Check the link below to check the details of Binary Heap-

Binary Heap Details

Max Binary Heap

Max Binary Heap
Max Binary Heap

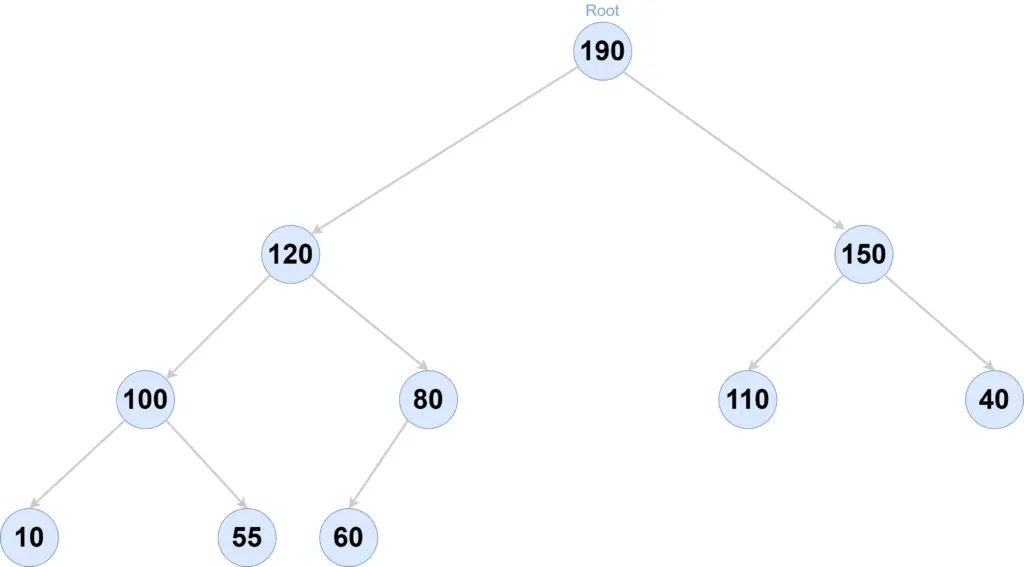
If we represent this Heap(binary tree) in an array, it will look like below-

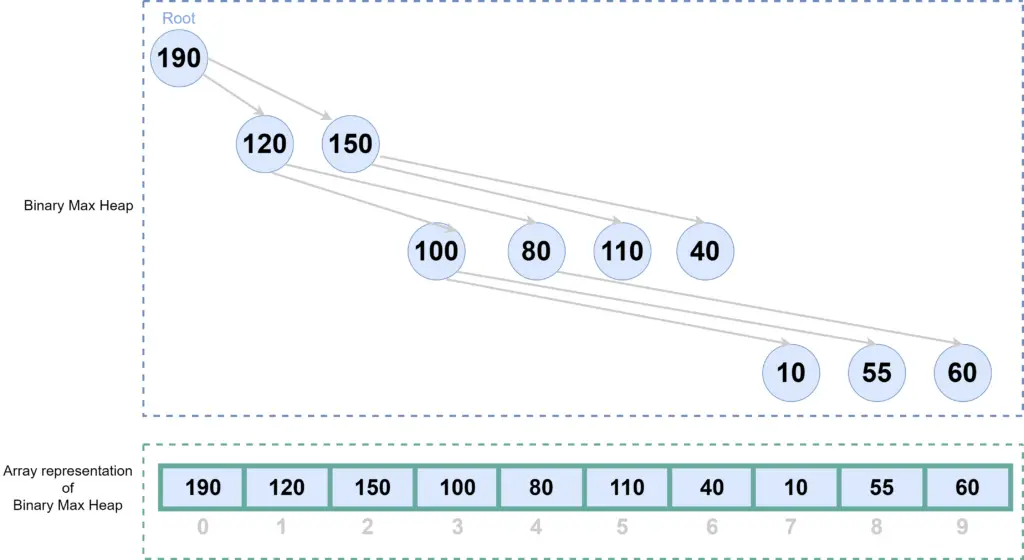
Binary Max Heap to array
Binary Max Heap to an array

Notice the indexes of the elements. Here can find the index of child elements from the index of parent, can find parent from the index of children, using the following formula-

  • If the parent element is in N th index, then-
    • Left child index: 2N + 1
    • Right child index: 2N + 2
  • If the child element is in N th index, then-
    • Parent element index: floor((N – 1) / 2)

Step #1: MaxBinaryHeap Class

class MaxBinaryHeap {
  constructor() {
    this.nodes = [];
  }
}

Step #2: Insert Method

class MaxBinaryHeap {
  // ...

  insert(data) {
    // assume the item will be inserted
    // at the end of the array initially
    let itemIndex = this.nodes.length;

    while (itemIndex > 0) {
      // Get the index of parent of the new data
      // Calculate by index
      // If index of an element is N, the then parent index is Floor((N - 1) / 2)
      const parentIndex = Math.floor((itemIndex - 1) / 2);

      // if current item is smaller than then parent then we are good
      // No changes required in that case
      if (parentIndex < 0 || this.nodes[parentIndex] > data) {
        break;
      }

      // if current item is larger than then parent
      // // then swap
      // if (this.nodes[parentIndex] < data) {
      this.nodes[itemIndex] = this.nodes[parentIndex];
      itemIndex = parentIndex;
      // }
    }

    // finally push the item in the selected index
    this.nodes[itemIndex] = data;

    return this.nodes;
  }
  
 //...
}

Step #3: Heapify Utility Method

class MaxBinaryHeap {
  // ...

  // Utility function to bring an element
  // to it's correct postion in a max heap
  heapify(currentIndex) {
    let largestIndex = currentIndex;
    let leftIndex = currentIndex * 2 + 1;
    let rightIndex = currentIndex * 2 + 2;

    if (
      leftIndex < this.nodes.length &&
      this.nodes[leftIndex] > this.nodes[largestIndex]
    ) {
      largestIndex = leftIndex;
    }

    if (
      rightIndex < this.nodes.length &&
      this.nodes[rightIndex] > this.nodes[largestIndex]
    ) {
      largestIndex = rightIndex;
    }

    // If either left or right node is larger than current node then swap
    if (largestIndex !== currentIndex) {
      const temp = this.nodes[currentIndex];
      this.nodes[currentIndex] = this.nodes[largestIndex];
      this.nodes[largestIndex] = temp;

      // Heapify the largest index element again
      this.heapify(largestIndex);
    }
  }
  
  // ...
}

Step #2: Extract Max Method

class MaxBinaryHeap {
  // ...

  // Extract the max item from the Heap
  extractMax() {
    // The max item is at the root
    // So extract and store that in a const
    const maxItem = this.nodes[0];

    // Get the last element
    const lastItem = this.nodes.pop();

    // Implement heapify if there are items left in the heap
    if (this.nodes.length > 0) {
      // Set the last item as the root (temporary)
      // The position is most probably not correct for this node
      // we are setting this for now
      // we will take it to the correct position in the next step
      this.nodes[0] = lastItem;

      // Bring the root element down if it is not the max item
      this.heapify(0);
    }

    // Return the extracted node
    return maxItem;
  }

  // ...
}

Full Source Code

// mbh.js
// Max Binary Heap implementation in JavaScript

class MaxBinaryHeap {
  constructor() {
    this.nodes = [];
  }

  // Insert item to the Heap
  insert(data) {
    // assume the item will be inserted
    // at the end of the array initially
    let itemIndex = this.nodes.length;

    while (itemIndex > 0) {
      // Get the index of parent of the new data
      // Calculate by index
      // If index of an element is N, the then parent index is Floor((N - 1) / 2)
      const parentIndex = Math.floor((itemIndex - 1) / 2);

      // if current item is smaller than then parent then we are good
      // No changes required in that case
      if (parentIndex < 0 || this.nodes[parentIndex] > data) {
        break;
      }

      this.nodes[itemIndex] = this.nodes[parentIndex];
      itemIndex = parentIndex;
    }

    // finally push the item in the selected index
    this.nodes[itemIndex] = data;

    return this.nodes;
  }

  // Extract the max item from the Heap
  extractMax() {
    // The max item is at the root
    // So extract and store that in a const
    const maxItem = this.nodes[0];

    // Get the last element
    const lastItem = this.nodes.pop();

    // Implement heapify if there are items left in the heap
    if (this.nodes.length > 0) {
      // Set the last item as the root (temporary)
      // The position is most probably not correct for this node
      // we are setting this for now
      // we will take it to the correct position in the next step
      this.nodes[0] = lastItem;

      // Bring the root element down if it is not the max item
      this.heapify(0);
    }

    // Return the extracted node
    return maxItem;
  }

  // Utility function to bring an element
  // to it's correct postion in a max heap
  heapify(currentIndex) {
    let largestIndex = currentIndex;
    let leftIndex = currentIndex * 2 + 1;
    let rightIndex = currentIndex * 2 + 2;

    if (
      leftIndex < this.nodes.length &&
      this.nodes[leftIndex] > this.nodes[largestIndex]
    ) {
      largestIndex = leftIndex;
    }

    if (
      rightIndex < this.nodes.length &&
      this.nodes[rightIndex] > this.nodes[largestIndex]
    ) {
      largestIndex = rightIndex;
    }

    // If either left or right node is larger than current node then swap
    if (largestIndex !== currentIndex) {
      const temp = this.nodes[currentIndex];
      this.nodes[currentIndex] = this.nodes[largestIndex];
      this.nodes[largestIndex] = temp;

      // Heapify the largest index element again
      this.heapify(largestIndex);
    }
  }
}

export default MaxBinaryHeap;

Demo

// demo.js
import MaxBinaryHeap from "./mbh.js";

// Create a new Max Binary Heap
let bigboxHeap = new MaxBinaryHeap();

console.log("\n\n----------- Max Binary Heap - Insert example -----------\n");

// Insert items
console.log("Insert - 190| Result: ", bigboxHeap.insert(190));
console.log("Insert - 100| Result: ", bigboxHeap.insert(100));
console.log("Insert - 120| Result: ", bigboxHeap.insert(120));
console.log("Insert - 150| Result: ", bigboxHeap.insert(150));
console.log("Insert - 80| Result: ", bigboxHeap.insert(80));
console.log("Insert - 110| Result: ", bigboxHeap.insert(110));
console.log("Insert - 40| Result: ", bigboxHeap.insert(40));
console.log("Insert - 10| Result: ", bigboxHeap.insert(10));
console.log("Insert - 55| Result: ", bigboxHeap.insert(55));
console.log("Insert - 60| Result: ", bigboxHeap.insert(60));

console.log(
  "\n\n----------- Max Binary Heap - Extract max example example -----------\n"
);

for (let i = 0; i < 12; i++) {
  console.log("Extract root | Result: ", bigboxHeap.extractMax());
}

Output:

----------- Max Binary Heap - Insert example -----------

Insert - 190| Result:  [ 190 ]
Insert - 100| Result:  [ 190, 100 ]
Insert - 120| Result:  [ 190, 100, 120 ]
Insert - 150| Result:  [ 190, 150, 120, 100 ]
Insert - 80| Result:  [ 190, 150, 120, 100, 80 ]
Insert - 110| Result:  [ 190, 150, 120, 100, 80, 110 ]
Insert - 40| Result:  [
  190, 150, 120,
  100,  80, 110,
   40
]
Insert - 10| Result:  [
  190, 150, 120, 100,
   80, 110,  40,  10
]
Insert - 55| Result:  [
  190, 150, 120, 100,
   80, 110,  40,  10,
   55
]
Insert - 60| Result:  [
  190, 150, 120, 100,
   80, 110,  40,  10,
   55,  60
]


----------- Max Binary Heap - Extract max example example -----------

Extract root | Result:  190
Extract root | Result:  150
Extract root | Result:  120
Extract root | Result:  110
Extract root | Result:  100
Extract root | Result:  80
Extract root | Result:  60
Extract root | Result:  55
Extract root | Result:  40
Extract root | Result:  10
Extract root | Result:  undefined
Extract root | Result:  undefined

Testing

// mbh.test.js
import { describe, it, beforeEach, expect } from "vitest";
import MaxBinaryHeap from "./mbh";

describe("MaxBinaryHeap", () => {
  let maxBinaryHeap;

    beforeEach(() => {
      maxBinaryHeap = new MaxBinaryHeap();
      maxBinaryHeap.insert(190);
      maxBinaryHeap.insert(100);
      maxBinaryHeap.insert(120);
      maxBinaryHeap.insert(150);
      maxBinaryHeap.insert(80);
      maxBinaryHeap.insert(110);
      maxBinaryHeap.insert(40);
      maxBinaryHeap.insert(10);
      maxBinaryHeap.insert(55);
      maxBinaryHeap.insert(60);
    });
  describe("Insert item to MaxBinaryHeap", () => {
    it("Should have correct length", () => {
      expect(maxBinaryHeap.nodes.length).toBe(10);
    });

    it("Should have correct sequence of items", () => {
      expect(maxBinaryHeap.nodes).toMatchObject([
        190, 150, 120, 100, 80, 110, 40, 10, 55, 60,
      ]);
    });
  });

  describe("Extract Max item to MaxBinaryHeap", () => {
    it("Should extract correct item", () => {
      expect(maxBinaryHeap.extractMax()).toBe(190);
      expect(maxBinaryHeap.extractMax()).toBe(150);
      expect(maxBinaryHeap.extractMax()).toBe(120);
      expect(maxBinaryHeap.extractMax()).toBe(110);
      expect(maxBinaryHeap.extractMax()).toBe(100);
      expect(maxBinaryHeap.extractMax()).toBe(80);
      expect(maxBinaryHeap.extractMax()).toBe(60);
      expect(maxBinaryHeap.extractMax()).toBe(55);
      expect(maxBinaryHeap.extractMax()).toBe(40);
      expect(maxBinaryHeap.extractMax()).toBe(10);
      expect(maxBinaryHeap.extractMax()).toBeUndefined();
    });
  });
});

Time Complexity

OperationComplexity
InsertO(log N)
Extract MaxO(log N)

Min Binary Heap

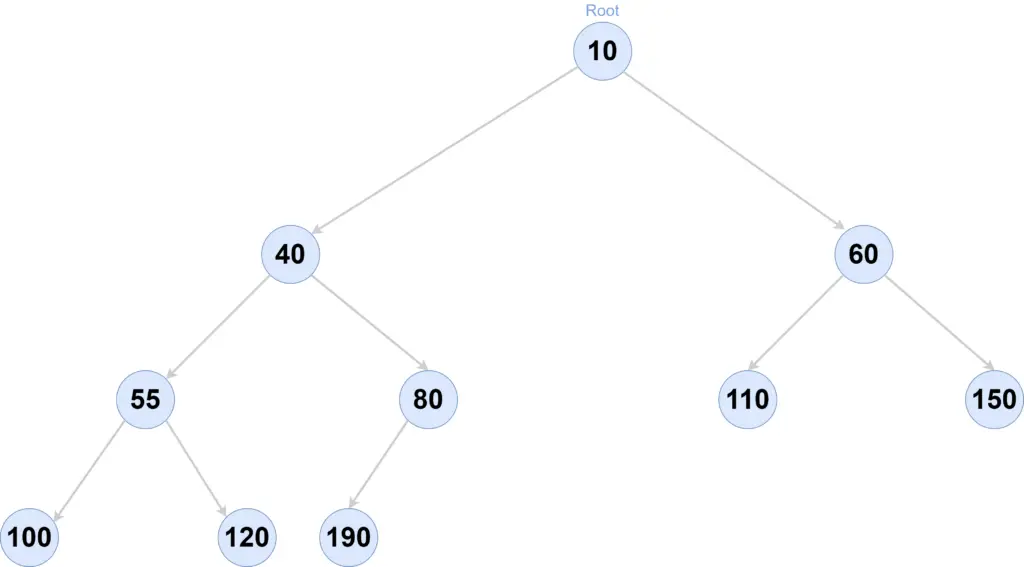
Min Binary Heap
Min Binary Heap

If we represent this Heap(binary tree) in an array, it will look like below-

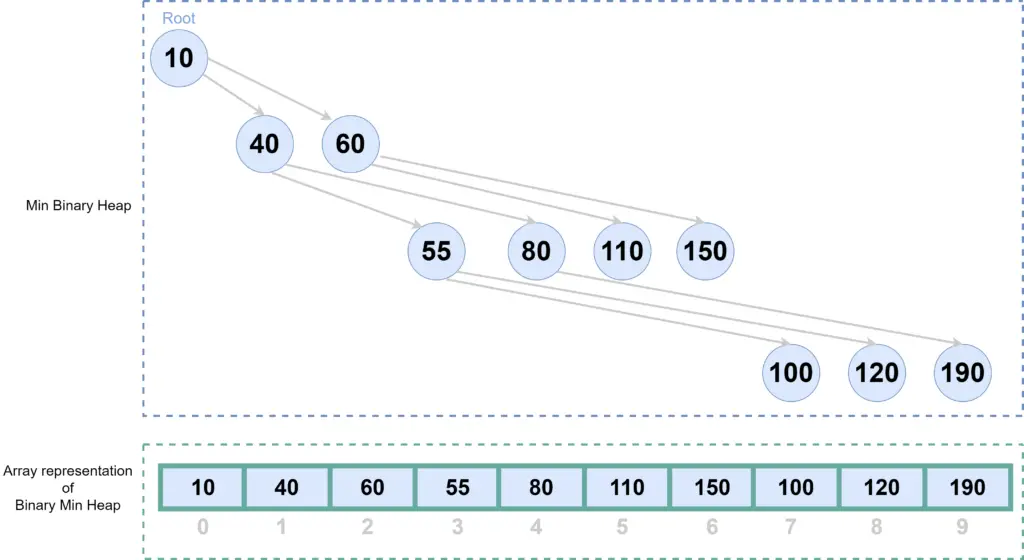
Min Binary Heap to Array
Min Binary Heap to Array

Notice the indexes of the elements. Here can find the index of child elements from the index of parent, can find parent from the index of children, using the following formula-

  • If parent element is in N th index, then-
    • Left child index: 2N + 1
    • Right child index: 2N + 2
  • If child element is in N th index, then-
    • Parent element index: floor((N – 1) / 2)

Step #1: MinBinaryHeap Class

class MinBinaryHeap {
  constructor() {
    this.nodes = [];
  }
}

Step #2: Insert Method

class MinBinaryHeap {
  // ...

  // Insert item to the Heap
  insert(data) {
    // assume the item will be inserted
    // at the end of the array initially
    let itemIndex = this.nodes.length;

    while (itemIndex > 0) {
      // Get the index of parent of the new data
      // Calculate by index
      // If index of an element is N, the then parent index is Floor((N - 1) / 2)
      const parentIndex = Math.floor((itemIndex - 1) / 2);

      // if current item is smaller than then parent then we are good
      // No changes required in that case
      if (parentIndex < 0 || this.nodes[parentIndex] < data) {
        break;
      }

      this.nodes[itemIndex] = this.nodes[parentIndex];
      itemIndex = parentIndex;
    }

    // finally push the item in the selected index
    this.nodes[itemIndex] = data;

    return this.nodes;
  }
  
 //...
}

Step #3: Heapify Utility Method

class MinBinaryHeap {
  // ...

  // Utility function to bring an element
  // to it's correct postion in a min heap
  heapify(currentIndex) {
    let largestIndex = currentIndex;
    let leftIndex = currentIndex * 2 + 1;
    let rightIndex = currentIndex * 2 + 2;

    if (
      leftIndex < this.nodes.length &&
      this.nodes[leftIndex] < this.nodes[largestIndex]
    ) {
      largestIndex = leftIndex;
    }

    if (
      rightIndex < this.nodes.length &&
      this.nodes[rightIndex] < this.nodes[largestIndex]
    ) {
      largestIndex = rightIndex;
    }

    // If either left or right node is larger than current node then swap
    if (largestIndex !== currentIndex) {
      const temp = this.nodes[currentIndex];
      this.nodes[currentIndex] = this.nodes[largestIndex];
      this.nodes[largestIndex] = temp;

      // Heapify the largest index element again
      this.heapify(largestIndex);
    }
  }
  
  // ...
}

Step #2: Extract Min Method

class MinBinaryHeap {
  // ...

  // Extract the min item from the Heap
  extractMin() {
    // The min item is at the root
    // So extract and store that in a const
    const minItem = this.nodes[0];

    // Get the last element
    const lastItem = this.nodes.pop();

    // Implement heapify if there are items left in the heap
    if (this.nodes.length > 0) {
      // Set the last item as the root (temporary)
      // The position is most probably not correct for this node
      // we are setting this for now
      // we will take it to the correct position in the next step
      this.nodes[0] = lastItem;

      // Bring the root element down if it is not the min item
      this.heapify(0);
    }

    // Return the extracted node
    return minItem;
  }

  // ...
}

Full Source Code

// mbh.js
// Min Binary Heap implementation in JavaScript

class MinBinaryHeap {
  constructor() {
    this.nodes = [];
  }

  // Insert item to the Heap
  insert(data) {
    // assume the item will be inserted
    // at the end of the array initially
    let itemIndex = this.nodes.length;

    while (itemIndex > 0) {
      // Get the index of parent of the new data
      // Calculate by index
      // If index of an element is N, the then parent index is Floor((N - 1) / 2)
      const parentIndex = Math.floor((itemIndex - 1) / 2);

      // if current item is smaller than then parent then we are good
      // No changes required in that case
      if (parentIndex < 0 || this.nodes[parentIndex] < data) {
        break;
      }

      this.nodes[itemIndex] = this.nodes[parentIndex];
      itemIndex = parentIndex;
    }

    // finally push the item in the selected index
    this.nodes[itemIndex] = data;

    return this.nodes;
  }

  // Extract the min item from the Heap
  extractMin() {
    // The min item is at the root
    // So extract and store that in a const
    const minItem = this.nodes[0];

    // Get the last element
    const lastItem = this.nodes.pop();

    // Implement heapify if there are items left in the heap
    if (this.nodes.length > 0) {
      // Set the last item as the root (temporary)
      // The position is most probably not correct for this node
      // we are setting this for now
      // we will take it to the correct position in the next step
      this.nodes[0] = lastItem;

      // Bring the root element down if it is not the min item
      this.heapify(0);
    }

    // Return the extracted node
    return minItem;
  }

  // Utility function to bring an element
  // to it's correct postion in a min heap
  heapify(currentIndex) {
    let largestIndex = currentIndex;
    let leftIndex = currentIndex * 2 + 1;
    let rightIndex = currentIndex * 2 + 2;

    if (
      leftIndex < this.nodes.length &&
      this.nodes[leftIndex] < this.nodes[largestIndex]
    ) {
      largestIndex = leftIndex;
    }

    if (
      rightIndex < this.nodes.length &&
      this.nodes[rightIndex] < this.nodes[largestIndex]
    ) {
      largestIndex = rightIndex;
    }

    // If either left or right node is larger than current node then swap
    if (largestIndex !== currentIndex) {
      const temp = this.nodes[currentIndex];
      this.nodes[currentIndex] = this.nodes[largestIndex];
      this.nodes[largestIndex] = temp;

      // Heapify the largest index element again
      this.heapify(largestIndex);
    }
  }
}

export default MinBinaryHeap;

Demo

// demo.js
import MinBinaryHeap from "./mbh.js";

// Create a new Min Binary Heap
let bigboxHeap = new MinBinaryHeap();

console.log("\n\n----------- Min Binary Heap - Insert example -----------\n");

// Insert items
console.log("Insert - 10| Result: ", bigboxHeap.insert(10));
console.log("Insert - 40| Result: ", bigboxHeap.insert(40));
console.log("Insert - 60| Result: ", bigboxHeap.insert(60));
console.log("Insert - 55| Result: ", bigboxHeap.insert(55));
console.log("Insert - 80| Result: ", bigboxHeap.insert(80));
console.log("Insert - 110| Result: ", bigboxHeap.insert(110));
console.log("Insert - 150| Result: ", bigboxHeap.insert(150));
console.log("Insert - 100| Result: ", bigboxHeap.insert(100));
console.log("Insert - 120| Result: ", bigboxHeap.insert(120));
console.log("Insert - 190| Result: ", bigboxHeap.insert(190));

console.log(
  "\n\n----------- Min Binary Heap - Extract max example -----------\n"
);

for (let i = 0; i < 12; i++) {
  console.log("Extract root | Result: ", bigboxHeap.extractMin());
}

Output:

----------- Min Binary Heap - Insert example -----------

Insert - 10| Result:  [ 10 ]
Insert - 40| Result:  [ 10, 40 ]
Insert - 60| Result:  [ 10, 40, 60 ]
Insert - 55| Result:  [ 10, 40, 60, 55 ]
Insert - 80| Result:  [ 10, 40, 60, 55, 80 ]
Insert - 110| Result:  [ 10, 40, 60, 55, 80, 110 ]
Insert - 150| Result:  [
  10,  40,  60, 55,
  80, 110, 150
]
Insert - 100| Result:  [
  10,  40,  60,  55,
  80, 110, 150, 100
]
Insert - 120| Result:  [
   10,  40,  60,  55,
   80, 110, 150, 100,
  120
]
Insert - 190| Result:  [
   10,  40,  60,  55,
   80, 110, 150, 100,
  120, 190
]


----------- Min Binary Heap - Extract max example -----------

Extract root | Result:  10
Extract root | Result:  40
Extract root | Result:  55
Extract root | Result:  60
Extract root | Result:  80
Extract root | Result:  100
Extract root | Result:  110
Extract root | Result:  120
Extract root | Result:  150
Extract root | Result:  190
Extract root | Result:  undefined
Extract root | Result:  undefined

Testing

// mbh.test.js
import { describe, it, beforeEach, expect } from "vitest";
import MinBinaryHeap from "./mbh";

describe("MinBinaryHeap", () => {
  let minBinaryHeap;

  beforeEach(() => {
    minBinaryHeap = new MinBinaryHeap();
    minBinaryHeap.insert(10);
    minBinaryHeap.insert(40);
    minBinaryHeap.insert(60);
    minBinaryHeap.insert(55);
    minBinaryHeap.insert(80);
    minBinaryHeap.insert(110);
    minBinaryHeap.insert(150);
    minBinaryHeap.insert(100);
    minBinaryHeap.insert(120);
    minBinaryHeap.insert(190);
  });
  describe("Insert item to MinBinaryHeap", () => {
    it("Should have correct length", () => {
      expect(minBinaryHeap.nodes.length).toBe(10);
    });

    it("Should have correct sequence of items", () => {
      expect(minBinaryHeap.nodes).toMatchObject([
        10, 40, 60, 55, 80, 110, 150, 100, 120, 190,
      ]);
    });
  });

  describe("Extract Min item to MinBinaryHeap", () => {
    it("Should extract correct item", () => {
      expect(minBinaryHeap.extractMin()).toBe(10);
      expect(minBinaryHeap.extractMin()).toBe(40);
      expect(minBinaryHeap.extractMin()).toBe(55);
      expect(minBinaryHeap.extractMin()).toBe(60);
      expect(minBinaryHeap.extractMin()).toBe(80);
      expect(minBinaryHeap.extractMin()).toBe(100);
      expect(minBinaryHeap.extractMin()).toBe(110);
      expect(minBinaryHeap.extractMin()).toBe(120);
      expect(minBinaryHeap.extractMin()).toBe(150);
      expect(minBinaryHeap.extractMin()).toBe(190);
      expect(minBinaryHeap.extractMin()).toBeUndefined();
    });
  });
});

Time Complexity

OperationComplexity
InsertO(log N)
Extract MinO(log N)

Source Code

Use the following links to get the source code used in this article-

Source Code ofImplementation CodeDemo CodeTest Code
JavaScript Implementation GitHub GitHub GitHub
TypeScript Implementation GitHub GitHub GitHub

Related Data Structures

CommandDetails
Singly Linked List Singly Linked List Detail

Other Code Implementations

Use the following links to check the BFS implementation in other programming languages-

Leave a Comment


The reCAPTCHA verification period has expired. Please reload the page.