Data Structure: Priority Queue in JavaScript and TypeScript

by

Priority queues are very frequently used data structures. Used to generate a queue so that we can process the items based on the priority of it.

NOTE

In this article, we are discussing the implementation of Priority Queue in JavaScript and TypeScript.

Check the link below to check the details of Priority Queue-

Priority Queue Details

Here we are using a Max Binary Heap to implement the Priority Queue. The code is mostly the same as Max Binary Heap, there are just a few differences-

Priority Queue using Max Binary Heap

Max Binary Heap
Priority Queue using Max Binary Heap

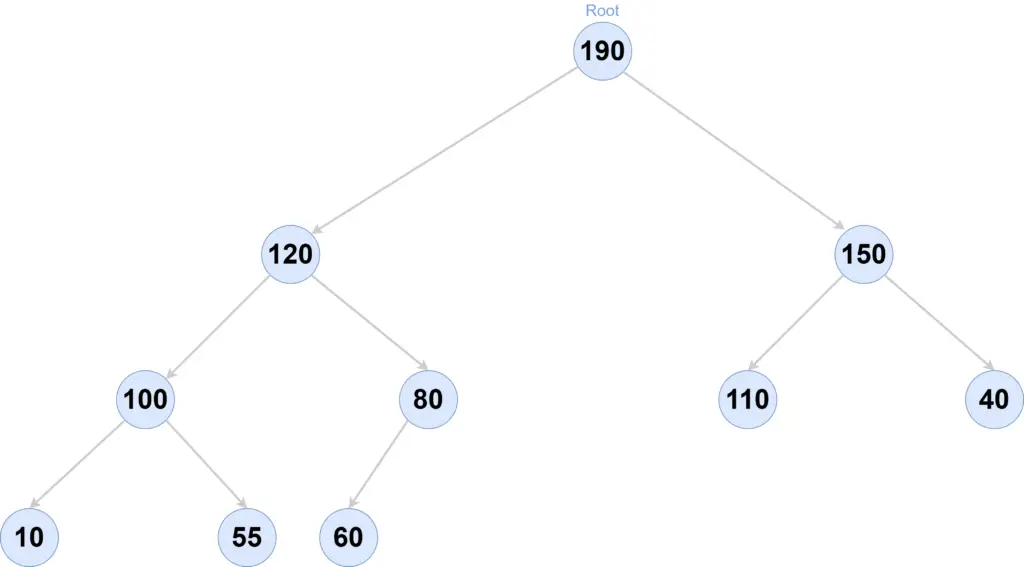
If we represent this Heap(binary tree) in an array, it will look like below-

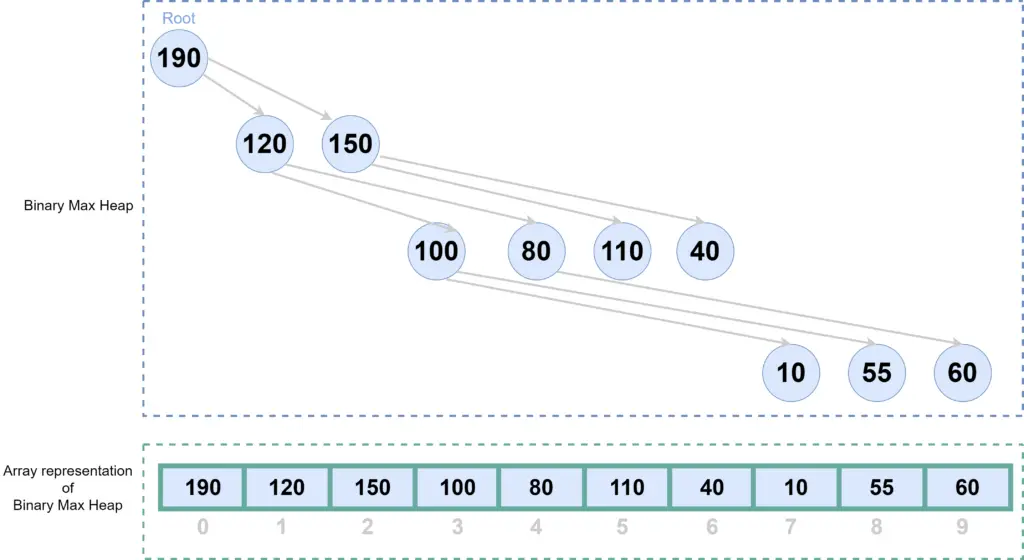
Binary Max Heap to array
Binary Max Heap to an array

Notice the indexes of the elements. Here can find the index of child elements from the index of parent, can find parent from the index of children, using the following formula-

  • If the parent element is in N th index, then-
    • Left child index: 2N + 1
    • Right child index: 2N + 2
  • If the child element is in N th index, then-
    • Parent element index: floor((N – 1) / 2)

Step #1: Node Class

Define class “Node”. This is used to store information of a single node.
Define fields – “data” and “priority”.
“data” field is used to store the actual data.
“priority” field is used to store the priority/importance of the node. In this case – the higher the priority value, the higher the importance is.
class Node {
  constructor(data, priority) {
    this.data = data;
    this.priority = priority;
  }
}

Step #2: Priority Queue Class

Define class “PriorityQueue”.
Define property “nodes”. This is used to store the list of nodes in the priority queue.
Initialize the “nodes” field with an empty array, in the constructor.
class PriorityQueue {
  constructor() {
    this.nodes = [];
  }
}

Step #3: Enqueue Method

Define method “enqueue”.
Accept “data” and “priority” as parameters.
Create a node from the “data” and “priority”.
Push the node at the end of the array.
Check if the parent is smaller than the newly added element. If the parent is smaller, then swap the new node with the parent. Keep swapping until the new node reached the correct position. 
class PriorityQueue {
  // ...

  // Insert item to the Heap
  enqueue(data, priority) {
    const newNode = new Node(data, priority);

    // assume the item will be inserted
    // at the end of the array initially
    let itemIndex = this.nodes.length;

    while (itemIndex > 0) {
      // Get the index of parent of the new data
      // Calculate by index
      // If index of an element is N, the then parent index is Floor((N - 1) / 2)
      const parentIndex = Math.floor((itemIndex - 1) / 2);

      // if current item is smaller than then parent then we are good
      // No changes required in that case
      if (parentIndex < 0 || this.nodes[parentIndex].priority > newNode.priority) {
        break;
      }

      this.nodes[itemIndex] = this.nodes[parentIndex];
      itemIndex = parentIndex;
    }

    // finally push the item in the selected index
    this.nodes[itemIndex] = newNode;

    return itemIndex;
  }
  
 //...
}

Step #4: Queue Position Setting Utility Method

Define method “setQueuePosition”. This method is used to move an item to the correct position based on the priority.

This function recursively calls itself until all the nodes reach the correct position.

class PriorityQueue {
  // ...

  // Utility function to bring an element
  // to it's correct postion
  setQueuePosition(currentIndex) {
    let largestIndex = currentIndex;
    let leftIndex = currentIndex * 2 + 1;
    let rightIndex = currentIndex * 2 + 2;

    if (
      leftIndex < this.nodes.length &&
      this.nodes[leftIndex].priority > this.nodes[largestIndex].priority
    ) {
      largestIndex = leftIndex;
    }

    if (
      rightIndex < this.nodes.length &&
      this.nodes[rightIndex].priority > this.nodes[largestIndex].priority
    ) {
      largestIndex = rightIndex;
    }

    // If either left or right node is larger than current node then swap
    if (largestIndex !== currentIndex) {
      const temp = this.nodes[currentIndex];
      this.nodes[currentIndex] = this.nodes[largestIndex];
      this.nodes[largestIndex] = temp;

      // setQueuePosition the largest index element again
      this.setQueuePosition(largestIndex);
    }
  }
  
  // ...
}

Step #5: Dequeue Method

Define method “dequeue”.
Return the current root, as this is the node with highest priority.
Then for the rest of the node, use the method “setQueuePosition” for putting the nodes to correct position.
class PriorityQueue {
  // ...

  // Extract the max item from the Heap
  dequeue() {
    // The max item is at the root
    // So extract and store that in a const
    const maxItem = this.nodes[0];

    // Get the last element
    const lastItem = this.nodes.pop();

    // Implement setQueuePosition if there are items left
    if (this.nodes.length > 0) {
      // Set the last item as the root (temporary)
      // The position is most probably not correct for this node
      // we are setting this for now
      // we will take it to the correct position in the next step
      this.nodes[0] = lastItem;

      // Bring the root element down if it is not the max item
      this.setQueuePosition(0);
    }

    // Return the extracted node
    return maxItem;
  }

  // ...
}

Full Source Code

Here is the full source code of the Priority Queue implementation-

// pq.js
// Priority Queue implementation in JavaScript

class Node {
  constructor(data, priority) {
    this.data = data;
    this.priority = priority;
  }
}

class PriorityQueue {
  constructor() {
    this.nodes = [];
  }

  // Insert item to the Heap
  enqueue(data, priority) {
    const newNode = new Node(data, priority);

    // assume the item will be inserted
    // at the end of the array initially
    let itemIndex = this.nodes.length;

    while (itemIndex > 0) {
      // Get the index of parent of the new data
      // Calculate by index
      // If index of an element is N, the then parent index is Floor((N - 1) / 2)
      const parentIndex = Math.floor((itemIndex - 1) / 2);

      // if current item is smaller than then parent then we are good
      // No changes required in that case
      if (parentIndex < 0 || this.nodes[parentIndex].priority > newNode.priority) {
        break;
      }

      this.nodes[itemIndex] = this.nodes[parentIndex];
      itemIndex = parentIndex;
    }

    // finally push the item in the selected index
    this.nodes[itemIndex] = newNode;

    return itemIndex;
  }

  // Extract the max item from the Heap
  dequeue() {
    // The max item is at the root
    // So extract and store that in a const
    const maxItem = this.nodes[0];

    // Get the last element
    const lastItem = this.nodes.pop();

    // Implement setQueuePosition if there are items left
    if (this.nodes.length > 0) {
      // Set the last item as the root (temporary)
      // The position is most probably not correct for this node
      // we are setting this for now
      // we will take it to the correct position in the next step
      this.nodes[0] = lastItem;

      // Bring the root element down if it is not the max item
      this.setQueuePosition(0);
    }

    // Return the extracted node
    return maxItem;
  }

  // Utility function to bring an element
  // to it's correct postion
  setQueuePosition(currentIndex) {
    let largestIndex = currentIndex;
    let leftIndex = currentIndex * 2 + 1;
    let rightIndex = currentIndex * 2 + 2;

    if (
      leftIndex < this.nodes.length &&
      this.nodes[leftIndex].priority > this.nodes[largestIndex].priority
    ) {
      largestIndex = leftIndex;
    }

    if (
      rightIndex < this.nodes.length &&
      this.nodes[rightIndex].priority > this.nodes[largestIndex].priority
    ) {
      largestIndex = rightIndex;
    }

    // If either left or right node is larger than current node then swap
    if (largestIndex !== currentIndex) {
      const temp = this.nodes[currentIndex];
      this.nodes[currentIndex] = this.nodes[largestIndex];
      this.nodes[largestIndex] = temp;

      // setQueuePosition the largest index element again
      this.setQueuePosition(largestIndex);
    }
  }
}

export default PriorityQueue;

Demo

Use the following code to check the implementation-

// demo.js
import PriorityQueue from "./pq.js";

// Create a new Priority Queue
let bigBoxPriorityQueue = new PriorityQueue();

console.log("\n----------- Priority Queue - Enqueue example -----------\n");

// Enqueue items
console.log("Enqueue - 100| Result Index: ", bigBoxPriorityQueue.enqueue('Shad Skiles', 100));
console.log("Enqueue - 150| Result Index: ", bigBoxPriorityQueue.enqueue('Isaias Hackett', 150));
console.log("Enqueue - 80| Result Index: ", bigBoxPriorityQueue.enqueue('Reggie Blick', 80));
console.log("Enqueue - 110| Result Index: ", bigBoxPriorityQueue.enqueue('Kali Feil', 110));
console.log("Enqueue - 40| Result Index: ", bigBoxPriorityQueue.enqueue('Jadyn Lesch', 40));
console.log("Enqueue - 120| Result Index: ", bigBoxPriorityQueue.enqueue('Candice Braun', 120));
console.log("Enqueue - 10| Result Index: ", bigBoxPriorityQueue.enqueue('Bailey Keeling', 10));
console.log("Enqueue - 190| Result Index: ", bigBoxPriorityQueue.enqueue('Jamil Bartoletti', 190));
console.log("Enqueue - 55| Result Index: ", bigBoxPriorityQueue.enqueue('Laurie Rowe', 55));
console.log("Enqueue - 60| Result Index: ", bigBoxPriorityQueue.enqueue('Jed Emard', 60));

console.log(
  "\n\n----------- Priority Queue - Dequeue example -----------\n"
);

for (let i = 0; i < 12; i++) {
  console.log("Dequeue | Result: ", bigBoxPriorityQueue.dequeue());
}

Output:

Here is the output of the demo code-

----------- Priority Queue - Enqueue example -----------

Enqueue - 100| Result Index:  0
Enqueue - 150| Result Index:  0
Enqueue - 80| Result Index:  2
Enqueue - 110| Result Index:  1
Enqueue - 40| Result Index:  4
Enqueue - 120| Result Index:  2
Enqueue - 10| Result Index:  6
Enqueue - 190| Result Index:  0
Enqueue - 55| Result Index:  8
Enqueue - 60| Result Index:  4


----------- Priority Queue - Dequeue example -----------

Dequeue | Result:  Node { data: 'Jamil Bartoletti', priority: 190 }
Dequeue | Result:  Node { data: 'Isaias Hackett', priority: 150 }
Dequeue | Result:  Node { data: 'Candice Braun', priority: 120 }
Dequeue | Result:  Node { data: 'Kali Feil', priority: 110 }
Dequeue | Result:  Node { data: 'Shad Skiles', priority: 100 }
Dequeue | Result:  Node { data: 'Reggie Blick', priority: 80 }
Dequeue | Result:  Node { data: 'Jed Emard', priority: 60 }
Dequeue | Result:  Node { data: 'Laurie Rowe', priority: 55 }
Dequeue | Result:  Node { data: 'Jadyn Lesch', priority: 40 }
Dequeue | Result:  Node { data: 'Bailey Keeling', priority: 10 }
Dequeue | Result:  undefined
Dequeue | Result:  undefined

Testing

Here are the tests for the Priority Queue implementation-

// pq.test.js
import { describe, it, beforeEach, expect } from "vitest";
import PriorityQueue from "./pq";

describe("Priority Queue", () => {
  let priorityQueue;

  beforeEach(() => {
    priorityQueue = new PriorityQueue();
    priorityQueue.enqueue("Shad Skiles", 100);
    priorityQueue.enqueue("Isaias Hackett", 150);
    priorityQueue.enqueue("Reggie Blick", 80);
    priorityQueue.enqueue("Kali Feil", 110);
    priorityQueue.enqueue("Jadyn Lesch", 40);
    priorityQueue.enqueue("Candice Braun", 120);
    priorityQueue.enqueue("Bailey Keeling", 10);
    priorityQueue.enqueue("Jamil Bartoletti", 190);
    priorityQueue.enqueue("Laurie Rowe", 55);
    priorityQueue.enqueue("Jed Emard", 60);
  });

  describe("Enqueue item to Priority Queue", () => {
    it("Should have correct length", () => {
      expect(priorityQueue.nodes.length).toBe(10);
    });

    it("Should have correct sequence of items", () => {
      expect(priorityQueue.nodes.map(node => node.priority)).toMatchObject([
        190, 150, 120, 110, 60, 80, 10, 100, 55, 40,
      ]);
    });
  });

  describe("Dequeue items from Priority Queue", () => {
    it("Should dequeue correct item", () => {
      expect(priorityQueue.dequeue().priority).toBe(190);
      expect(priorityQueue.dequeue().priority).toBe(150);
      expect(priorityQueue.dequeue().priority).toBe(120);
      expect(priorityQueue.dequeue().priority).toBe(110);
      expect(priorityQueue.dequeue().priority).toBe(100);
      expect(priorityQueue.dequeue().priority).toBe(80);
      expect(priorityQueue.dequeue().priority).toBe(60);
      expect(priorityQueue.dequeue().priority).toBe(55);
      expect(priorityQueue.dequeue().priority).toBe(40);
      expect(priorityQueue.dequeue().priority).toBe(10);
      expect(priorityQueue.dequeue()).toBeUndefined();
    });
  });
});

Time Complexity

OperationComplexity
InsertO(log N)
Extract MaxO(log N)

Source Code

Use the following links to get the source code used in this article-

Source Code ofImplementation CodeDemo CodeTest Code
JavaScript Implementation GitHub GitHub GitHub
TypeScript Implementation GitHub GitHub GitHub

Related Data Structures

CommandDetails
Binary Heap Binary Heap

Other Code Implementations

Use the following links to check the BFS implementation in other programming languages-

Leave a Comment


The reCAPTCHA verification period has expired. Please reload the page.