A binary Heap is a special kind of tree. For a Binary Tree to be a Binary Heap the rule is simple-
As we can see, there are 2 types of Binary Heap- min and max.
![]() NOTE
NOTE
In this article, we are discussing the implementation of Binary Heap(both Min and Max) in JavaScript and TypeScript.
Max Binary Heap
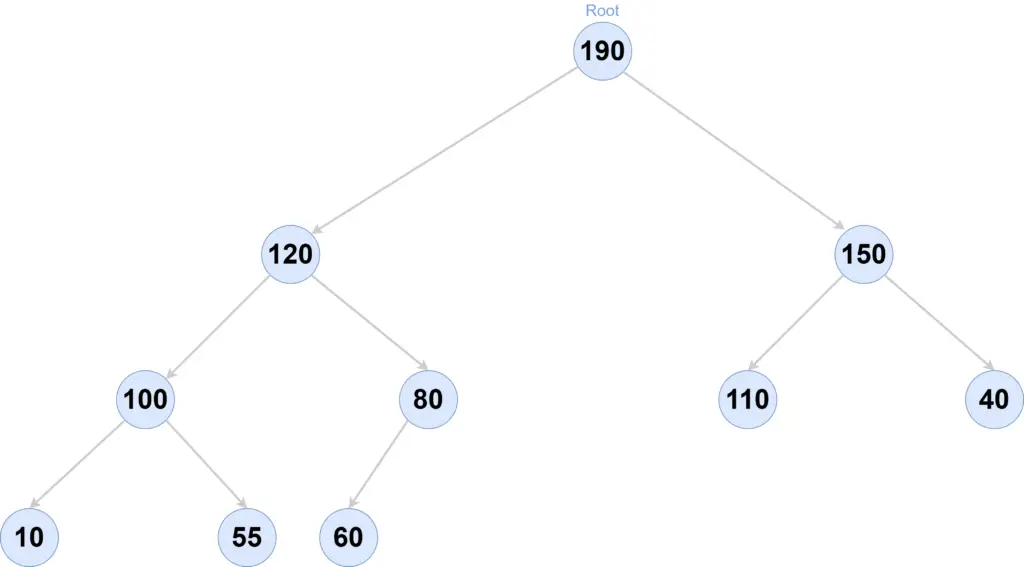
If we represent this Heap(binary tree) in an array, it will look like below-
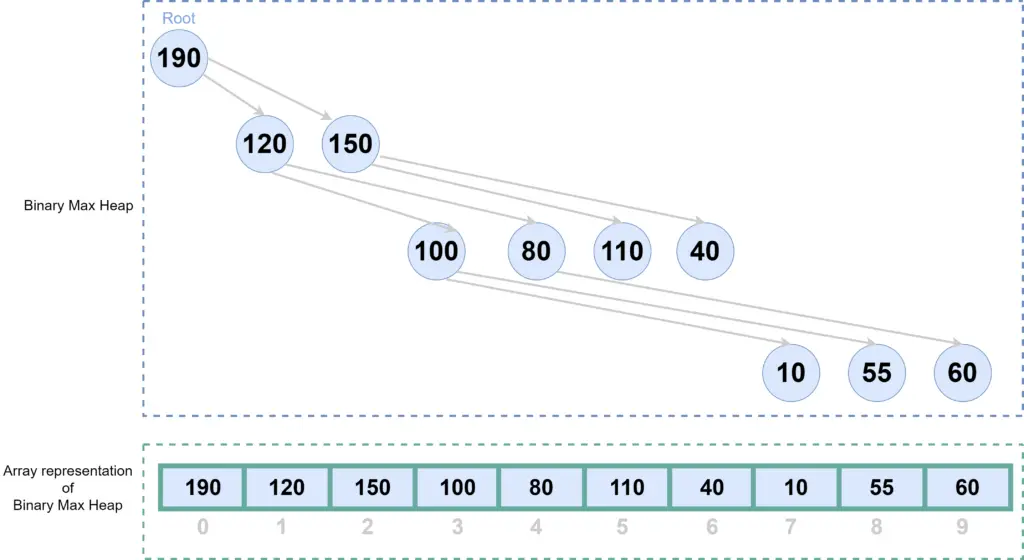
Notice the indexes of the elements. Here can find the index of child elements from the index of parent, can find parent from the index of children, using the following formula-
- If the parent element is in N th index, then-
- Left child index: 2N + 1
- Right child index: 2N + 2
- If the child element is in N th index, then-
- Parent element index: floor((N – 1) / 2)
Step #1: MaxBinaryHeap Class
class MaxBinaryHeap {
constructor() {
this.nodes = [];
}
}Step #2: Insert Method
class MaxBinaryHeap {
// .... other part of code
// Insert item to the Heap
insert(data) {
// assume the item will be inserted
// at the end of the array initially
let itemIndex = this.nodes.length;
while (itemIndex > 0) {
// Get the index of parent of the new data
// Calculate by index
// If index of an element is N, the then parent index is Floor((N - 1) / 2)
const parentIndex = Math.floor((itemIndex - 1) / 2);
// if current item is smaller than then parent then we are good
// No changes required in that case
if (parentIndex < 0 || this.nodes[parentIndex] > data) {
break;
}
this.nodes[itemIndex] = this.nodes[parentIndex];
itemIndex = parentIndex;
}
// finally push the item in the selected index
this.nodes[itemIndex] = data;
return this.nodes;
}
// .... other part of code
}
export default MaxBinaryHeap;
Step #3: Heapify Utility Method
class MaxBinaryHeap {
// .... other part of code
// Utility function to bring an element
// to it's correct postion in a max heap
heapify(currentIndex) {
let largestIndex = currentIndex;
let leftIndex = currentIndex * 2 + 1;
let rightIndex = currentIndex * 2 + 2;
if (
leftIndex < this.nodes.length &&
this.nodes[leftIndex] > this.nodes[largestIndex]
) {
largestIndex = leftIndex;
}
if (
rightIndex < this.nodes.length &&
this.nodes[rightIndex] > this.nodes[largestIndex]
) {
largestIndex = rightIndex;
}
// If either left or right node is larger than current node then swap
if (largestIndex !== currentIndex) {
const temp = this.nodes[currentIndex];
this.nodes[currentIndex] = this.nodes[largestIndex];
this.nodes[largestIndex] = temp;
// Heapify the largest index element again
this.heapify(largestIndex);
}
}
// .... other part of code
}
Step #2: Extract Max Method
class MaxBinaryHeap {
// .... other part of code
// Extract the max item from the Heap
extractMax() {
// The max item is at the root
// So extract and store that in a const
const maxItem = this.nodes[0];
// Get the last element
const lastItem = this.nodes.pop();
// Implement heapify if there are items left in the heap
if (this.nodes.length > 0) {
// Set the last item as the root (temporary)
// The position is most probably not correct for this node
// we are setting this for now
// we will take it to the correct position in the next step
this.nodes[0] = lastItem;
// Bring the root element down if it is not the max item
this.heapify(0);
}
// Return the extracted node
return maxItem;
}
// .... other part of code
}Full Source Code
// mbh.js
// Max Binary Heap implementation in JavaScript
class MaxBinaryHeap {
constructor() {
this.nodes = [];
}
// Insert item to the Heap
insert(data) {
// assume the item will be inserted
// at the end of the array initially
let itemIndex = this.nodes.length;
while (itemIndex > 0) {
// Get the index of parent of the new data
// Calculate by index
// If index of an element is N, the then parent index is Floor((N - 1) / 2)
const parentIndex = Math.floor((itemIndex - 1) / 2);
// if current item is smaller than then parent then we are good
// No changes required in that case
if (parentIndex < 0 || this.nodes[parentIndex] > data) {
break;
}
this.nodes[itemIndex] = this.nodes[parentIndex];
itemIndex = parentIndex;
}
// finally push the item in the selected index
this.nodes[itemIndex] = data;
return this.nodes;
}
// Extract the max item from the Heap
extractMax() {
// The max item is at the root
// So extract and store that in a const
const maxItem = this.nodes[0];
// Get the last element
const lastItem = this.nodes.pop();
// Implement heapify if there are items left in the heap
if (this.nodes.length > 0) {
// Set the last item as the root (temporary)
// The position is most probably not correct for this node
// we are setting this for now
// we will take it to the correct position in the next step
this.nodes[0] = lastItem;
// Bring the root element down if it is not the max item
this.heapify(0);
}
// Return the extracted node
return maxItem;
}
// Utility function to bring an element
// to it's correct postion in a max heap
heapify(currentIndex) {
let largestIndex = currentIndex;
let leftIndex = currentIndex * 2 + 1;
let rightIndex = currentIndex * 2 + 2;
if (
leftIndex < this.nodes.length &&
this.nodes[leftIndex] > this.nodes[largestIndex]
) {
largestIndex = leftIndex;
}
if (
rightIndex < this.nodes.length &&
this.nodes[rightIndex] > this.nodes[largestIndex]
) {
largestIndex = rightIndex;
}
// If either left or right node is larger than current node then swap
if (largestIndex !== currentIndex) {
const temp = this.nodes[currentIndex];
this.nodes[currentIndex] = this.nodes[largestIndex];
this.nodes[largestIndex] = temp;
// Heapify the largest index element again
this.heapify(largestIndex);
}
}
}
export default MaxBinaryHeap;
Demo
// demo.js
import MaxBinaryHeap from "./mbh.js";
// Create a new Max Binary Heap
let bigboxHeap = new MaxBinaryHeap();
console.log("\n\n----------- Max Binary Heap - Insert example -----------\n");
// Insert items
console.log("Insert - 190| Result: ", bigboxHeap.insert(190));
console.log("Insert - 100| Result: ", bigboxHeap.insert(100));
console.log("Insert - 120| Result: ", bigboxHeap.insert(120));
console.log("Insert - 150| Result: ", bigboxHeap.insert(150));
console.log("Insert - 80| Result: ", bigboxHeap.insert(80));
console.log("Insert - 110| Result: ", bigboxHeap.insert(110));
console.log("Insert - 40| Result: ", bigboxHeap.insert(40));
console.log("Insert - 10| Result: ", bigboxHeap.insert(10));
console.log("Insert - 55| Result: ", bigboxHeap.insert(55));
console.log("Insert - 60| Result: ", bigboxHeap.insert(60));
console.log(
"\n\n----------- Max Binary Heap - Extract max example example -----------\n"
);
for (let i = 0; i < 12; i++) {
console.log("Extract root | Result: ", bigboxHeap.extractMax());
}
Output:
u002du002du002du002du002du002du002du002du002du002d- Max Binary Heap - Insert example u002du002du002du002du002du002du002du002du002du002d-nnInsert - 190| Result: [ 190 ]nInsert - 100| Result: [ 190, 100 ]nInsert - 120| Result: [ 190, 100, 120 ]nInsert - 150| Result: [ 190, 150, 120, 100 ]nInsert - 80| Result: [ 190, 150, 120, 100, 80 ]nInsert - 110| Result: [ 190, 150, 120, 100, 80, 110 ]nInsert - 40| Result: [n 190, 150, 120,n 100, 80, 110,n 40n]nInsert - 10| Result: [n 190, 150, 120, 100,n 80, 110, 40, 10n]nInsert - 55| Result: [n 190, 150, 120, 100,n 80, 110, 40, 10,n 55n]nInsert - 60| Result: [n 190, 150, 120, 100,n 80, 110, 40, 10,n 55, 60n]nnnu002du002du002du002du002du002du002du002du002du002d- Max Binary Heap - Extract max example example u002du002du002du002du002du002du002du002du002du002d-nnExtract root | Result: 190nExtract root | Result: 150nExtract root | Result: 120nExtract root | Result: 110nExtract root | Result: 100nExtract root | Result: 80nExtract root | Result: 60nExtract root | Result: 55nExtract root | Result: 40nExtract root | Result: 10nExtract root | Result: undefinednExtract root | Result: undefinedTesting
// mbh.test.js
import { describe, it, beforeEach, expect } from "vitest";
import MaxBinaryHeap from "./mbh";
describe("MaxBinaryHeap", () => {
let maxBinaryHeap;
beforeEach(() => {
maxBinaryHeap = new MaxBinaryHeap();
maxBinaryHeap.insert(190);
maxBinaryHeap.insert(100);
maxBinaryHeap.insert(120);
maxBinaryHeap.insert(150);
maxBinaryHeap.insert(80);
maxBinaryHeap.insert(110);
maxBinaryHeap.insert(40);
maxBinaryHeap.insert(10);
maxBinaryHeap.insert(55);
maxBinaryHeap.insert(60);
});
describe("Insert item to MaxBinaryHeap", () => {
it("Should have correct length", () => {
expect(maxBinaryHeap.nodes.length).toBe(10);
});
it("Should have correct sequence of items", () => {
expect(maxBinaryHeap.nodes).toMatchObject([
190, 150, 120, 100, 80, 110, 40, 10, 55, 60,
]);
});
});
describe("Extract Max item to MaxBinaryHeap", () => {
it("Should extract correct item", () => {
expect(maxBinaryHeap.extractMax()).toBe(190);
expect(maxBinaryHeap.extractMax()).toBe(150);
expect(maxBinaryHeap.extractMax()).toBe(120);
expect(maxBinaryHeap.extractMax()).toBe(110);
expect(maxBinaryHeap.extractMax()).toBe(100);
expect(maxBinaryHeap.extractMax()).toBe(80);
expect(maxBinaryHeap.extractMax()).toBe(60);
expect(maxBinaryHeap.extractMax()).toBe(55);
expect(maxBinaryHeap.extractMax()).toBe(40);
expect(maxBinaryHeap.extractMax()).toBe(10);
expect(maxBinaryHeap.extractMax()).toBeUndefined();
});
});
});
Time Complexity
| Operation | Complexity |
|---|---|
| Insert | O(log N) |
| Extract Max | O(log N) |
Min Binary Heap
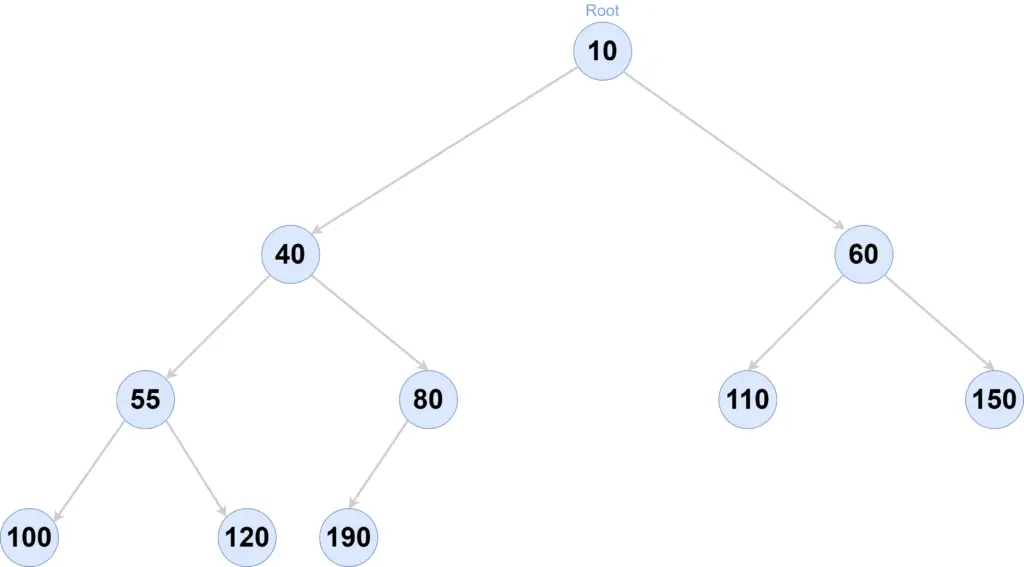
If we represent this Heap(binary tree) in an array, it will look like below-
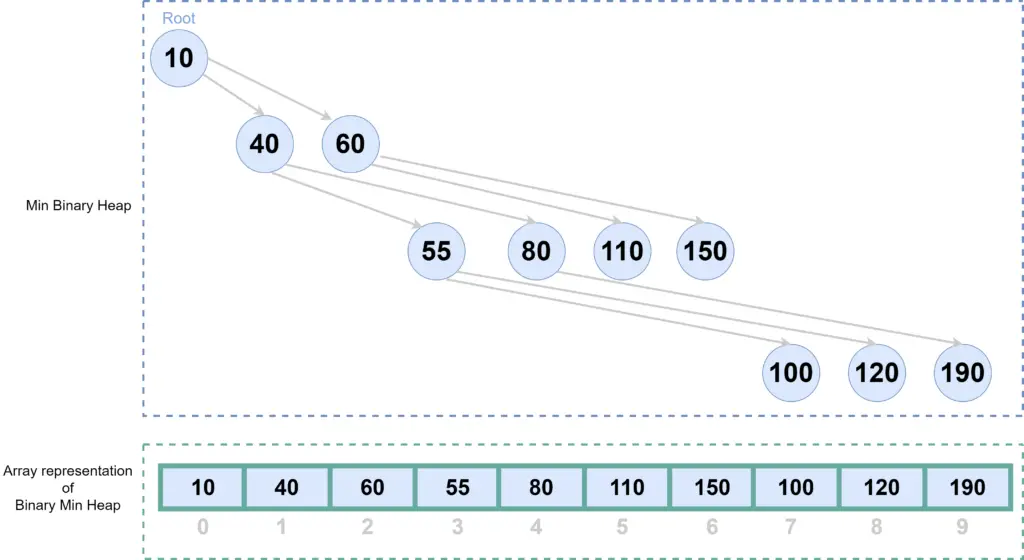
Notice the indexes of the elements. Here can find the index of child elements from the index of parent, can find parent from the index of children, using the following formula-
- If parent element is in N th index, then-
- Left child index: 2N + 1
- Right child index: 2N + 2
- If child element is in N th index, then-
- Parent element index: floor((N – 1) / 2)
Step #1: MinBinaryHeap Class
class MinBinaryHeap {
constructor() {
this.nodes = [];
}
// ... other methods here
}Step #2: Insert Method
class MinBinaryHeap {
// ... other methods here
// Insert item to the Heap
insert(data) {
// assume the item will be inserted
// at the end of the array initially
let itemIndex = this.nodes.length;
while (itemIndex > 0) {
// Get the index of parent of the new data
// Calculate by index
// If index of an element is N, the then parent index is Floor((N - 1) / 2)
const parentIndex = Math.floor((itemIndex - 1) / 2);
// if current item is smaller than then parent then we are good
// No changes required in that case
if (parentIndex < 0 || this.nodes[parentIndex] < data) {
break;
}
this.nodes[itemIndex] = this.nodes[parentIndex];
itemIndex = parentIndex;
}
// finally push the item in the selected index
this.nodes[itemIndex] = data;
return this.nodes;
}
// ... other methods here
}Step #3: Heapify Utility Method
class MinBinaryHeap {
// ... other methods here
// Utility function to bring an element
// to it's correct postion in a min heap
heapify(currentIndex) {
let largestIndex = currentIndex;
let leftIndex = currentIndex * 2 + 1;
let rightIndex = currentIndex * 2 + 2;
if (
leftIndex < this.nodes.length &&
this.nodes[leftIndex] < this.nodes[largestIndex]
) {
largestIndex = leftIndex;
}
if (
rightIndex < this.nodes.length &&
this.nodes[rightIndex] < this.nodes[largestIndex]
) {
largestIndex = rightIndex;
}
// If either left or right node is larger than current node then swap
if (largestIndex !== currentIndex) {
const temp = this.nodes[currentIndex];
this.nodes[currentIndex] = this.nodes[largestIndex];
this.nodes[largestIndex] = temp;
// Heapify the largest index element again
this.heapify(largestIndex);
}
}
}Step #2: Extract Min Method
class MinBinaryHeap {
// ... other methods here
// Extract the min item from the Heap
extractMin() {
// The min item is at the root
// So extract and store that in a const
const minItem = this.nodes[0];
// Get the last element
const lastItem = this.nodes.pop();
// Implement heapify if there are items left in the heap
if (this.nodes.length > 0) {
// Set the last item as the root (temporary)
// The position is most probably not correct for this node
// we are setting this for now
// we will take it to the correct position in the next step
this.nodes[0] = lastItem;
// Bring the root element down if it is not the min item
this.heapify(0);
}
// Return the extracted node
return minItem;
}
// ... other methods here
}Full Source Code
// mbh.js
// Min Binary Heap implementation in JavaScript
class MinBinaryHeap {
constructor() {
this.nodes = [];
}
// Insert item to the Heap
insert(data) {
// assume the item will be inserted
// at the end of the array initially
let itemIndex = this.nodes.length;
while (itemIndex > 0) {
// Get the index of parent of the new data
// Calculate by index
// If index of an element is N, the then parent index is Floor((N - 1) / 2)
const parentIndex = Math.floor((itemIndex - 1) / 2);
// if current item is smaller than then parent then we are good
// No changes required in that case
if (parentIndex < 0 || this.nodes[parentIndex] < data) {
break;
}
this.nodes[itemIndex] = this.nodes[parentIndex];
itemIndex = parentIndex;
}
// finally push the item in the selected index
this.nodes[itemIndex] = data;
return this.nodes;
}
// Extract the min item from the Heap
extractMin() {
// The min item is at the root
// So extract and store that in a const
const minItem = this.nodes[0];
// Get the last element
const lastItem = this.nodes.pop();
// Implement heapify if there are items left in the heap
if (this.nodes.length > 0) {
// Set the last item as the root (temporary)
// The position is most probably not correct for this node
// we are setting this for now
// we will take it to the correct position in the next step
this.nodes[0] = lastItem;
// Bring the root element down if it is not the min item
this.heapify(0);
}
// Return the extracted node
return minItem;
}
// Utility function to bring an element
// to it's correct postion in a min heap
heapify(currentIndex) {
let largestIndex = currentIndex;
let leftIndex = currentIndex * 2 + 1;
let rightIndex = currentIndex * 2 + 2;
if (
leftIndex < this.nodes.length &&
this.nodes[leftIndex] < this.nodes[largestIndex]
) {
largestIndex = leftIndex;
}
if (
rightIndex < this.nodes.length &&
this.nodes[rightIndex] < this.nodes[largestIndex]
) {
largestIndex = rightIndex;
}
// If either left or right node is larger than current node then swap
if (largestIndex !== currentIndex) {
const temp = this.nodes[currentIndex];
this.nodes[currentIndex] = this.nodes[largestIndex];
this.nodes[largestIndex] = temp;
// Heapify the largest index element again
this.heapify(largestIndex);
}
}
}
export default MinBinaryHeap;
Demo
// demo.js
import MinBinaryHeap from "./mbh.js";
// Create a new Min Binary Heap
let bigboxHeap = new MinBinaryHeap();
console.log("\n\n----------- Min Binary Heap - Insert example -----------\n");
// Insert items
console.log("Insert - 10| Result: ", bigboxHeap.insert(10));
console.log("Insert - 40| Result: ", bigboxHeap.insert(40));
console.log("Insert - 60| Result: ", bigboxHeap.insert(60));
console.log("Insert - 55| Result: ", bigboxHeap.insert(55));
console.log("Insert - 80| Result: ", bigboxHeap.insert(80));
console.log("Insert - 110| Result: ", bigboxHeap.insert(110));
console.log("Insert - 150| Result: ", bigboxHeap.insert(150));
console.log("Insert - 100| Result: ", bigboxHeap.insert(100));
console.log("Insert - 120| Result: ", bigboxHeap.insert(120));
console.log("Insert - 190| Result: ", bigboxHeap.insert(190));
console.log(
"\n\n----------- Min Binary Heap - Extract max example -----------\n"
);
for (let i = 0; i < 12; i++) {
console.log("Extract root | Result: ", bigboxHeap.extractMin());
}
Output:
----------- Min Binary Heap - Insert example -----------
Insert - 10| Result: [ 10 ]
Insert - 40| Result: [ 10, 40 ]
Insert - 60| Result: [ 10, 40, 60 ]
Insert - 55| Result: [ 10, 40, 60, 55 ]
Insert - 80| Result: [ 10, 40, 60, 55, 80 ]
Insert - 110| Result: [ 10, 40, 60, 55, 80, 110 ]
Insert - 150| Result: [
10, 40, 60, 55,
80, 110, 150
]
Insert - 100| Result: [
10, 40, 60, 55,
80, 110, 150, 100
]
Insert - 120| Result: [
10, 40, 60, 55,
80, 110, 150, 100,
120
]
Insert - 190| Result: [
10, 40, 60, 55,
80, 110, 150, 100,
120, 190
]
----------- Min Binary Heap - Extract max example -----------
Extract root | Result: 10
Extract root | Result: 40
Extract root | Result: 55
Extract root | Result: 60
Extract root | Result: 80
Extract root | Result: 100
Extract root | Result: 110
Extract root | Result: 120
Extract root | Result: 150
Extract root | Result: 190
Extract root | Result: undefined
Extract root | Result: undefinedTesting
// mbh.test.js
import { describe, it, beforeEach, expect } from "vitest";
import MinBinaryHeap from "./mbh";
describe("MinBinaryHeap", () => {
let minBinaryHeap;
beforeEach(() => {
minBinaryHeap = new MinBinaryHeap();
minBinaryHeap.insert(10);
minBinaryHeap.insert(40);
minBinaryHeap.insert(60);
minBinaryHeap.insert(55);
minBinaryHeap.insert(80);
minBinaryHeap.insert(110);
minBinaryHeap.insert(150);
minBinaryHeap.insert(100);
minBinaryHeap.insert(120);
minBinaryHeap.insert(190);
});
describe("Insert item to MinBinaryHeap", () => {
it("Should have correct length", () => {
expect(minBinaryHeap.nodes.length).toBe(10);
});
it("Should have correct sequence of items", () => {
expect(minBinaryHeap.nodes).toMatchObject([
10, 40, 60, 55, 80, 110, 150, 100, 120, 190,
]);
});
});
describe("Extract Min item to MinBinaryHeap", () => {
it("Should extract correct item", () => {
expect(minBinaryHeap.extractMin()).toBe(10);
expect(minBinaryHeap.extractMin()).toBe(40);
expect(minBinaryHeap.extractMin()).toBe(55);
expect(minBinaryHeap.extractMin()).toBe(60);
expect(minBinaryHeap.extractMin()).toBe(80);
expect(minBinaryHeap.extractMin()).toBe(100);
expect(minBinaryHeap.extractMin()).toBe(110);
expect(minBinaryHeap.extractMin()).toBe(120);
expect(minBinaryHeap.extractMin()).toBe(150);
expect(minBinaryHeap.extractMin()).toBe(190);
expect(minBinaryHeap.extractMin()).toBeUndefined();
});
});
});
Time Complexity
| Operation | Complexity |
|---|---|
| Insert | O(log N) |
| Extract Min | O(log N) |
Source Code
Use the following links to get the source code used in this article-
| Source Code of | Implementation Code | Demo Code | Test Code |
|---|---|---|---|
| JavaScript Implementation | |||
| TypeScript Implementation |
Related Data Structures
| Command | Details |
|---|---|
| Singly Linked List |
Other Code Implementations
Use the following links to check the BFS implementation in other programming languages-



