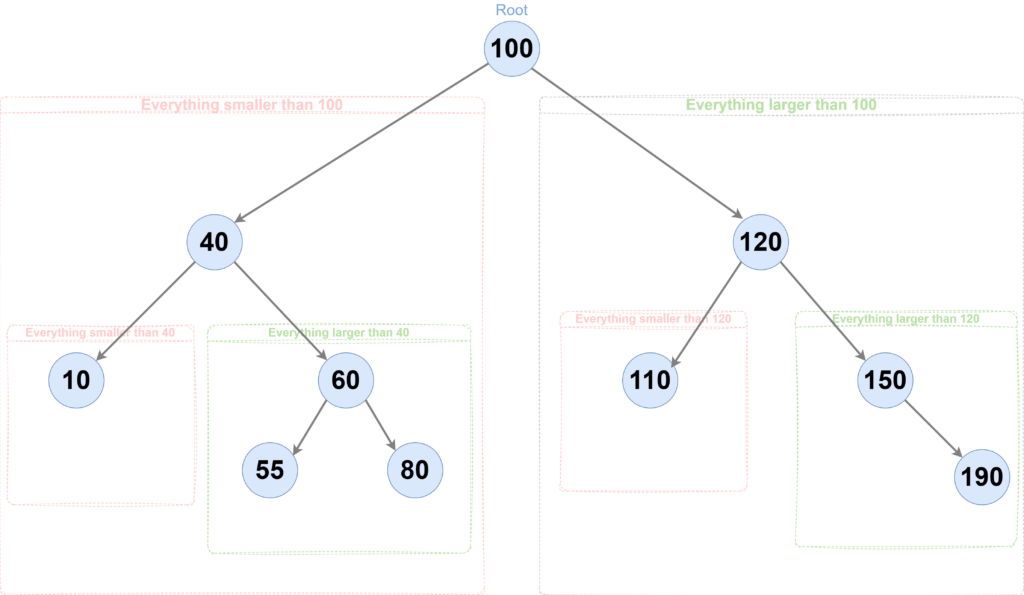
Data Structure: Binary Search Tree(BST)

by

Binary Search Tree or BST is a special type of tree that is used for organizing data in a way that makes searching easier. The rule is simple for BST-

  • Everything on the left of the node is smaller than the selected node.
  • Everything on the right of the node is larger than the selected node.
Binary Search Tree(BST)
Binary Search Tree(BST)

Implementation #1: Simple Implementation

Let’s go with the simple approach, to implement Binary Search tree-

Step #1: Node Class

class Node {
  constructor(data) {
    this.data = data;
    this.left = null;
    this.right = null;
  }
}
JavaScript
class Node<T> {
  private data: T;
  private left: Node<T> | null;
  private right: Node<T> | null;

  constructor(data: T) {
    this.data = data;
    this.left = null;
    this.right = null;
  }

  public getData(): T {
    return this.data;
  }

  public getLeft(): Node<T> | null {
    return this.left;
  }

  public setLeft(left: Node<T>): void {
    this.left = left;
  }

  public getRight(): Node<T> | null {
    return this.right;
  }

  public setRight(right: Node<T>): void {
    this.right = right;
  }
}
TypeScript

Step #2: BinarySearchTree Class

class BinarySearchTree {
  constructor() {
    this.root = null;
  }
}
JavaScript
class BinarySearchTree<T> {
  private root: Node<T> | null;

  constructor() {
    this.root = null;
  }
}
TypeScript

Step #3: Insert Operation

class BinarySearchTree {
  //...
  
  insert(data) {
    const newNode = new Node(data);

    // If there is no root, then make new node as head
    if (!this.root) {
      this.root = newNode;
      return this;
    }

    let currentNode = this.root;

    while (currentNode) {
      // If node with same data already exists
      // then do nothing
      if(data === currentNode.data) break;

      // If data is smaller then go left
      if (data < currentNode.data) {
        // If the left is empty
        // then insert this new node on the left
        if (!currentNode.left) {
          currentNode.left = newNode;

          break;
        }

        // If there is node on the left
        // then go to the left node
        currentNode = currentNode.left;
      } else {
        // If data is larger then go right

        // If no node on then right
        // then insert on right
        if (!currentNode.right) {
          currentNode.right = newNode;
          break;
        }

        // If there is node on the right
        // then go to the right node
        currentNode = currentNode.right;
      }
    }

    return this;
  }
  
  //...
}
JavaScript
class BinarySearchTree<T> {
  //...
  
  insert(data: T) {
    const newNode = new Node(data);

    // If there is no root, then make new node as head
    if (!this.root) {
      this.root = newNode;
      return this;
    }

    let currentNode: Node<T> | null = this.root;

    while (currentNode) {
      // If node with same data already exists
      // then do nothing
      if (data === currentNode.getData()) break;

      // If data is smaller then go left
      if (data < currentNode.getData()) {
        // If the left is empty
        // then insert this new node on the left
        if (!currentNode.getLeft()) {
          currentNode.setLeft(newNode);

          break;
        }

        // If there is node on the left
        // then go to the left node
        currentNode = currentNode.getLeft();
      } else {
        // If data is larger then go right

        // If no node on then right
        // then insert on right
        if (!currentNode.getRight()) {
          currentNode.setRight(newNode);
          break;
        }

        // If there is node on the right
        // then go to the right node
        currentNode = currentNode.getRight();
      }
    }

    return this;
  }
  
  //...
}
TypeScript

Step #4: Search Operation

class BinarySearchTree {
  //...
  
  search(data) {
    let currentNode = this.root;

    while(currentNode) {
      // console.log(currentNode.data);
      if (data === currentNode.data) {
        return currentNode;
      }

      if (data < currentNode.data) {
        currentNode = currentNode.left;
      } else {
        currentNode = currentNode.right;
      }
    }

    return currentNode;
  }
  
  //...
}
JavaScript
class BinarySearchTree<T> {
  //...
  
  search(data: T) {
    let currentNode = this.root;

    while (currentNode) {
      // console.log(currentNode.data);
      if (data === currentNode.getData()) {
        return currentNode;
      }

      if (data < currentNode.getData()) {
        currentNode = currentNode.getLeft();
      } else {
        currentNode = currentNode.getRight();
      }
    }

    return currentNode;
  }
  
  //...
}
TypeScript

Full Source Code

class Node {
  constructor(data) {
    this.data = data;
    this.left = null;
    this.right = null;
  }
}

class BinarySearchTree {
  constructor() {
    this.root = null;
  }

  insert(data) {
    const newNode = new Node(data);

    // If there is no root, then make new node as head
    if (!this.root) {
      this.root = newNode;
      return this;
    }

    let currentNode = this.root;

    while (currentNode) {
      // If node with same data already exists
      // then do nothing
      if(data === currentNode.data) break;

      // If data is smaller then go left
      if (data < currentNode.data) {
        // If the left is empty
        // then insert this new node on the left
        if (!currentNode.left) {
          currentNode.left = newNode;

          break;
        }

        // If there is node on the left
        // then go to the left node
        currentNode = currentNode.left;
      } else {
        // If data is larger then go right

        // If no node on then right
        // then insert on right
        if (!currentNode.right) {
          currentNode.right = newNode;
          break;
        }

        // If there is node on the right
        // then go to the right node
        currentNode = currentNode.right;
      }
    }

    return this;
  }

  search(data) {
    let currentNode = this.root;

    while(currentNode) {
      // console.log(currentNode.data);
      if (data === currentNode.data) {
        return currentNode;
      }

      if (data < currentNode.data) {
        currentNode = currentNode.left;
      } else {
        currentNode = currentNode.right;
      }
    }

    return currentNode;
  }
}
JavaScript
class Node<T> {
  private data: T;
  private left: Node<T> | null;
  private right: Node<T> | null;

  constructor(data: T) {
    this.data = data;
    this.left = null;
    this.right = null;
  }

  public getData(): T {
    return this.data;
  }

  public getLeft(): Node<T> | null {
    return this.left;
  }

  public setLeft(left: Node<T>): void {
    this.left = left;
  }

  public getRight(): Node<T> | null {
    return this.right;
  }

  public setRight(right: Node<T>): void {
    this.right = right;
  }
}

class BinarySearchTree<T> {
  private root: Node<T> | null;

  constructor() {
    this.root = null;
  }

  insert(data: T) {
    const newNode = new Node(data);

    // If there is no root, then make new node as head
    if (!this.root) {
      this.root = newNode;
      return this;
    }

    let currentNode: Node<T> | null = this.root;

    while (currentNode) {
      // If node with same data already exists
      // then do nothing
      if (data === currentNode.getData()) break;

      // If data is smaller then go left
      if (data < currentNode.getData()) {
        // If the left is empty
        // then insert this new node on the left
        if (!currentNode.getLeft()) {
          currentNode.setLeft(newNode);

          break;
        }

        // If there is node on the left
        // then go to the left node
        currentNode = currentNode.getLeft();
      } else {
        // If data is larger then go right

        // If no node on then right
        // then insert on right
        if (!currentNode.getRight()) {
          currentNode.setRight(newNode);
          break;
        }

        // If there is node on the right
        // then go to the right node
        currentNode = currentNode.getRight();
      }
    }

    return this;
  }

  search(data: T) {
    let currentNode = this.root;

    while (currentNode) {
      // console.log(currentNode.data);
      if (data === currentNode.getData()) {
        return currentNode;
      }

      if (data < currentNode.getData()) {
        currentNode = currentNode.getLeft();
      } else {
        currentNode = currentNode.getRight();
      }
    }

    return currentNode;
  }
}
TypeScript

Demo

// demo.js
import BinarySearchTree from "./bst.js";

// Create a new Stack
let bigboxBST = new BinarySearchTree();

console.log("\n\n----------- BST insert example -----------\n");

// Push items
console.log('Insert - 100 | Result: ', bigboxBST.insert(100));
console.log('Insert - 40 | Result: ', bigboxBST.insert(40));
console.log('Insert - 60 | Result: ', bigboxBST.insert(60));
console.log('Insert - 190 | Result: ', bigboxBST.insert(190));
console.log('Insert - 110 | Result: ', bigboxBST.insert(110));
console.log('Insert - 150 | Result: ', bigboxBST.insert(150));
console.log('Insert - 120 | Result: ', bigboxBST.insert(120));
console.log('Insert - 100 | Result: ', bigboxBST.insert(100));


console.log(bigboxBST);

console.log("\n\n----------- BST search example -----------\n");

console.log(bigboxBST.search(150));
console.log(bigboxBST.search(130));
console.log(bigboxBST.search(60));
JavaScript
// demo.ts
import BinarySearchTree from "./bst";

// Create a new Stack
let bigboxBST = new BinarySearchTree<number>();

console.log("\n\n----------- BST insert example -----------\n");

// Push items
console.log('Insert - 100 | Result: ', bigboxBST.insert(100));
console.log('Insert - 40 | Result: ', bigboxBST.insert(40));
console.log('Insert - 60 | Result: ', bigboxBST.insert(60));
console.log('Insert - 190 | Result: ', bigboxBST.insert(190));
console.log('Insert - 110 | Result: ', bigboxBST.insert(110));
console.log('Insert - 150 | Result: ', bigboxBST.insert(150));
console.log('Insert - 120 | Result: ', bigboxBST.insert(120));
console.log('Insert - 100 | Result: ', bigboxBST.insert(100));


console.log(bigboxBST);

console.log("\n\n----------- BST search example -----------\n");

console.log(bigboxBST.search(150));
console.log(bigboxBST.search(130));
console.log(bigboxBST.search(60));
TypeScript

Output:

----------- BST insert example -----------
Insert - 100 | Result:  BinarySearchTree { root: Node { data: 100, left: null, right: null } }
Insert - 40 | Result:  BinarySearchTree {
  root: Node {
    data: 100,
    left: Node { data: 40, left: null, right: null },
    right: null
  }
}
Insert - 60 | Result:  BinarySearchTree {
  root: Node {
    data: 100,
    left: Node { data: 40, left: null, right: [Node] },
    right: null
  }
}
Insert - 190 | Result:  BinarySearchTree {
  root: Node {
    data: 100,
    left: Node { data: 40, left: null, right: [Node] },
    right: Node { data: 190, left: null, right: null }
  }
}
Insert - 110 | Result:  BinarySearchTree {
  root: Node {
    data: 100,
    left: Node { data: 40, left: null, right: [Node] },
    right: Node { data: 190, left: [Node], right: null }
  }
}
Insert - 150 | Result:  BinarySearchTree {
  root: Node {
    data: 100,
    left: Node { data: 40, left: null, right: [Node] },
    right: Node { data: 190, left: [Node], right: null }
  }
}
Insert - 120 | Result:  BinarySearchTree {
  root: Node {
    data: 100,
    left: Node { data: 40, left: null, right: [Node] },
    right: Node { data: 190, left: [Node], right: null }
  }
}
Insert - 100 | Result:  BinarySearchTree {
  root: Node {
    data: 100,
    left: Node { data: 40, left: null, right: [Node] },
    right: Node { data: 190, left: [Node], right: null }
  }
}
BinarySearchTree {
  root: Node {
    data: 100,
    left: Node { data: 40, left: null, right: [Node] },
    right: Node { data: 190, left: [Node], right: null }
  }
}
----------- BST search example -----------
Node {
  data: 150,
  left: Node { data: 120, left: null, right: null },
  right: null
}
null
Node { data: 60, left: null, right: null }
Plaintext

Implementation #2: With Recursion

In this approach we are using recursion in our code, to make the code easier to implement and read-

Step #1: Node Class

The Node class will be same. We have no change here.

class Node {
  constructor(data) {
    this.data = data;
    this.left = null;
    this.right = null;
  }
}
JavaScript
class Node<T> {
  private data: T;
  private left: Node<T> | null;
  private right: Node<T> | null;

  constructor(data: T) {
    this.data = data;
    this.left = null;
    this.right = null;
  }

  public getData(): T {
    return this.data;
  }

  public getLeft(): Node<T> | null {
    return this.left;
  }

  public setLeft(left: Node<T>): void {
    this.left = left;
  }

  public getRight(): Node<T> | null {
    return this.right;
  }

  public setRight(right: Node<T>): void {
    this.right = right;
  }
}
TypeScript

Step #2: BinarySearchTree Class

The BinarySearchTree has the same property as the simple approach, no change here.

class BinarySearchTree {
  //...
  
  insert(data) {
    const newNode = new Node(data);

    if (this.root === null) {
      this.root = newNode;
    } else {
      this.insertNode(this.root, newNode);
    }

    return this;
  }
  
  insertNode(currentNode, newNode) {
    // If data is smaller, then go left
    if (newNode.data < currentNode.data) {
      // If left is empty then insert the new node here
      if (currentNode.left === null) {
        currentNode.left = newNode;
      } else {
        // Go even further if there are nodes on the left
        this.insertNode(currentNode.left, newNode); // Recursive call
      }
    } else {
      // If data is larger, then go right
      if (currentNode.right === null) {
        currentNode.right = newNode;
      } else {
        // Go right if there are nodes on right
        this.insertNode(currentNode.right, newNode); // Recursive call
      }
    }
  }

  //...
}
JavaScript
class BinarySearchTree<T> {
  private root: Node<T> | null;

  constructor() {
    this.root = null;
  }
}
TypeScript

Step #3: Insert Operation

class BinarySearchTree {
  //...
  
  insert(data) {
    const newNode = new Node(data);

    if (this.root === null) {
      this.root = newNode;
    } else {
      this.insertNode(this.root, newNode);
    }

    return this;
  }
  
  insertNode(currentNode, newNode) {
    // If data is smaller, then go left
    if (newNode.data < currentNode.data) {
      // If left is empty then insert the new node here
      if (currentNode.left === null) {
        currentNode.left = newNode;
      } else {
        // Go even further if there are nodes on the left
        this.insertNode(currentNode.left, newNode); // Recursive call
      }
    } else {
      // If data is larger, then go right
      if (currentNode.right === null) {
        currentNode.right = newNode;
      } else {
        // Go right if there are nodes on right
        this.insertNode(currentNode.right, newNode); // Recursive call
      }
    }
  }

  //...
}
JavaScript
class BinarySearchTree<T> {
  //...
  
  insert(data: T) {
    const newNode = new Node(data);

    // Insertion function to be called recursively
    const insertNode = (currentNode: Node<T> | null, newNode: Node<T>) => {
      if (currentNode === null) return;

      // If data is smaller, then go left
      if (newNode.getData() < currentNode.getData()) {
        // If left is empty then insert the new node here
        if (currentNode.getLeft() === null) {
          currentNode.setLeft(newNode);
        } else {
          // Go even further if there are nodes on the left
          insertNode(currentNode.getLeft(), newNode); // Recursive call
        }
      } else {
        // If data is larger, then go right
        if (currentNode.getRight() === null) {
          currentNode.setRight(newNode);
        } else {
          // Go right if there are nodes on right
          insertNode(currentNode.getRight(), newNode); // Recursive call
        }
      }
    };

    if (this.root === null) {
      this.root = newNode;
    } else {
      insertNode(this.root, newNode);
    }

    return this;
  }
  
  //...
}
TypeScript

Step #4: Search Operation

class BinarySearchTree {
  //...
  
  // Main search function
  search(data) {
    return this.searchNode(this.root, data);
  }

  // Search function to be called recursively
  searchNode(currentNode, data) {
    // If the node is null, that means we have reached some end
    // and still have not found any node with the provided data
    if (currentNode === null) {
      return null;
    }

    // Go left if data is samller
    if (data < currentNode.data) {
      return this.searchNode(currentNode.left, data); // Recursive call
    }

    // Go right if data is larger
    if (data > currentNode.data) {
      return this.searchNode(currentNode.right, data); // Recursive call
    }

    return currentNode;
  }
  
  //...
}
JavaScript
class BinarySearchTree<T> {
  //...
  
  search(data: T): Node<T> | null {
    // Search function to be called recursively
    const searchNode = (currentNode: Node<T> | null, data: T): Node<T> | null => {
      // If the node is null, that means we have reached some end
      // and still have not found any node with the provided data
      if (currentNode === null) {
        return null;
      }

      // Go left if data is samller
      if (data < currentNode.getData()) {
        return searchNode(currentNode.getLeft(), data); // Recursive call
      }

      // Go right if data is larger
      if (data > currentNode.getData()) {
        return searchNode(currentNode.getRight(), data); // Recursive call
      }

      return currentNode;
    };

    return searchNode(this.root, data);
  }
  
  //...
}
TypeScript

Full Source Code

class Node {
  constructor(data) {
    this.data = data;
    this.left = null;
    this.right = null;
  }
}

class BinarySearchTree {
  constructor() {
    this.root = null;
  }

  // Main insert function to initialize the insertion
  insert(data) {
    const newNode = new Node(data);

    if (this.root === null) {
      this.root = newNode;
    } else {
      this.insertNode(this.root, newNode);
    }

    return this;
  }

  // Insertion function to be called recursively
  insertNode(currentNode, newNode) {
    // If data is smaller, then go left
    if (newNode.data < currentNode.data) {
      // If left is empty then insert the new node here
      if (currentNode.left === null) {
        currentNode.left = newNode;
      } else {
        // Go even further if there are nodes on the left
        this.insertNode(currentNode.left, newNode); // Recursive call
      }
    } else {
      // If data is larger, then go right
      if (currentNode.right === null) {
        currentNode.right = newNode;
      } else {
        // Go right if there are nodes on right
        this.insertNode(currentNode.right, newNode); // Recursive call
      }
    }
  }

  // Main search function
  search(data) {
    return this.searchNode(this.root, data);
  }

  // Search function to be called recursively
  searchNode(currentNode, data) {
    // If the node is null, that means we have reached some end
    // and still have not found any node with the provided data
    if (currentNode === null) {
      return null;
    }

    // Go left if data is samller
    if (data < currentNode.data) {
      return this.searchNode(currentNode.left, data); // Recursive call
    }

    // Go right if data is larger
    if (data > currentNode.data) {
      return this.searchNode(currentNode.right, data); // Recursive call
    }

    return currentNode;
  }
}
JavaScript
class Node<T> {
  private data: T;
  private left: Node<T> | null;
  private right: Node<T> | null;

  constructor(data: T) {
    this.data = data;
    this.left = null;
    this.right = null;
  }

  public getData(): T {
    return this.data;
  }

  public getLeft(): Node<T> | null {
    return this.left;
  }

  public setLeft(left: Node<T>): void {
    this.left = left;
  }

  public getRight(): Node<T> | null {
    return this.right;
  }

  public setRight(right: Node<T>): void {
    this.right = right;
  }
}

class BinarySearchTree<T> {
  private root: Node<T> | null;

  constructor() {
    this.root = null;
  }

  // Main insert function to initialize the insertion
  insert(data: T) {
    const newNode = new Node(data);

    // Insertion function to be called recursively
    const insertNode = (currentNode: Node<T> | null, newNode: Node<T>) => {
      if (currentNode === null) return;

      // If data is smaller, then go left
      if (newNode.getData() < currentNode.getData()) {
        // If left is empty then insert the new node here
        if (currentNode.getLeft() === null) {
          currentNode.setLeft(newNode);
        } else {
          // Go even further if there are nodes on the left
          insertNode(currentNode.getLeft(), newNode); // Recursive call
        }
      } else {
        // If data is larger, then go right
        if (currentNode.getRight() === null) {
          currentNode.setRight(newNode);
        } else {
          // Go right if there are nodes on right
          insertNode(currentNode.getRight(), newNode); // Recursive call
        }
      }
    };

    if (this.root === null) {
      this.root = newNode;
    } else {
      insertNode(this.root, newNode);
    }

    return this;
  }

  // Main search function
  search(data: T): Node<T> | null {
    // Search function to be called recursively
    const searchNode = (currentNode: Node<T> | null, data: T): Node<T> | null => {
      // If the node is null, that means we have reached some end
      // and still have not found any node with the provided data
      if (currentNode === null) {
        return null;
      }

      // Go left if data is samller
      if (data < currentNode.getData()) {
        return searchNode(currentNode.getLeft(), data); // Recursive call
      }

      // Go right if data is larger
      if (data > currentNode.getData()) {
        return searchNode(currentNode.getRight(), data); // Recursive call
      }

      return currentNode;
    };

    return searchNode(this.root, data);
  }
}
TypeScript

Demo

// demo.js
import BinarySearchTree from "./bst.js";

// Create a new Stack
let bigboxBST = new BinarySearchTree();

console.log("\n\n----------- BST insert example -----------\n");

// Push items
console.log('Insert - 100 | Result: ', bigboxBST.insert(100));
console.log('Insert - 40 | Result: ', bigboxBST.insert(40));
console.log('Insert - 60 | Result: ', bigboxBST.insert(60));
console.log('Insert - 190 | Result: ', bigboxBST.insert(190));
console.log('Insert - 110 | Result: ', bigboxBST.insert(110));
console.log('Insert - 150 | Result: ', bigboxBST.insert(150));
console.log('Insert - 120 | Result: ', bigboxBST.insert(120));
console.log('Insert - 100 | Result: ', bigboxBST.insert(100));


console.log(bigboxBST);


console.log("\n\n----------- BST search example -----------\n");

console.log(bigboxBST.search(150));
console.log(bigboxBST.search(130));
console.log(bigboxBST.search(60));
JavaScript
// demo.ts
import BinarySearchTree from "./bst";

// Create a new Stack
let bigboxBST = new BinarySearchTree<number>();

console.log("\n\n----------- BST insert example -----------\n");

// Push items
console.log('Insert - 100 | Result: ', bigboxBST.insert(100));
console.log('Insert - 40 | Result: ', bigboxBST.insert(40));
console.log('Insert - 60 | Result: ', bigboxBST.insert(60));
console.log('Insert - 190 | Result: ', bigboxBST.insert(190));
console.log('Insert - 110 | Result: ', bigboxBST.insert(110));
console.log('Insert - 150 | Result: ', bigboxBST.insert(150));
console.log('Insert - 120 | Result: ', bigboxBST.insert(120));
console.log('Insert - 100 | Result: ', bigboxBST.insert(100));


console.log(bigboxBST);


console.log("\n\n----------- BST search example -----------\n");

console.log(bigboxBST.search(150));
console.log(bigboxBST.search(130));
console.log(bigboxBST.search(60));
TypeScript

Output:

----------- BST insert example -----------
Insert - 100 | Result:  BinarySearchTree { root: Node { data: 100, left: null, right: null } }
Insert - 40 | Result:  BinarySearchTree {
  root: Node {
    data: 100,
    left: Node { data: 40, left: null, right: null },
    right: null
  }
}
Insert - 60 | Result:  BinarySearchTree {
  root: Node {
    data: 100,
    left: Node { data: 40, left: null, right: [Node] },
    right: null
  }
}
Insert - 190 | Result:  BinarySearchTree {
  root: Node {
    data: 100,
    left: Node { data: 40, left: null, right: [Node] },
    right: Node { data: 190, left: null, right: null }
  }
}
Insert - 110 | Result:  BinarySearchTree {
  root: Node {
    data: 100,
    left: Node { data: 40, left: null, right: [Node] },
    right: Node { data: 190, left: [Node], right: null }
  }
}
Insert - 150 | Result:  BinarySearchTree {
  root: Node {
    data: 100,
    left: Node { data: 40, left: null, right: [Node] },
    right: Node { data: 190, left: [Node], right: null }
  }
}
Insert - 120 | Result:  BinarySearchTree {
  root: Node {
    data: 100,
    left: Node { data: 40, left: null, right: [Node] },
    right: Node { data: 190, left: [Node], right: null }
  }
}
Insert - 100 | Result:  BinarySearchTree {
  root: Node {
    data: 100,
    left: Node { data: 40, left: null, right: [Node] },
    right: Node { data: 190, left: [Node], right: null }
  }
}
BinarySearchTree {
  root: Node {
    data: 100,
    left: Node { data: 40, left: null, right: [Node] },
    right: Node { data: 190, left: [Node], right: null }
  }
}
----------- BST search example -----------
Node {
  data: 150,
  left: Node { data: 120, left: null, right: null },
  right: null
}
null
Node { data: 60, left: null, right: null }
Plaintext

Time Complexity

OperationComplexity
InsertO(log(n))
SearchO(log(n))

Source Code

Use the following links to get the source code used in this article-

Source Code ofImplementation CodeDemo CodeTest Code
JavaScript Implementation GitHub GitHub GitHub
TypeScript Implementation GitHub GitHub GitHub

Related Data Structures

CommandDetails
Singly Linked List Singly Linked List Detail

Leave a Comment


The reCAPTCHA verification period has expired. Please reload the page.